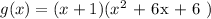Question

For the polynomial below, -1 is a zero.g(x) = x + 7x² + 12x + 6Express g (x) as a product of linear factors.

Answer 1

Step 1 :

In this question, we are given that x = - 1 is a zero of the polynomial:

`g(x)=x^3+7x^2\text{ + 12 x + 6}`

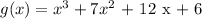
If x = - 1 is a zero of the polynomial, then x + 1 is a factor of :

`g(x)=x^3+7x^2\text{ + 7 x + 6}`

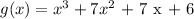
Step 2 :

`\begin{gathered} \text{Then, we have that:} \\ \frac{x^3+7x^2\text{ + 12 x + 6}}{x\text{ + 1}} \\ =x^2\text{ + 6 x + 6} \end{gathered}`

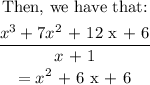
Step 3 :

Expressing g( x ) as a product of linear factors, we have that:

`\begin{gathered} \text{If g ( x ) = }x^3+7x^2\text{ +12 x + 6,} \\ \text{then g ( x ) = ( x + 1 ) ( x}^2\text{ + 6 x + 6 )} \end{gathered}`

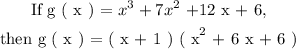
CONCLUSION:

Expressing g ( x ) as a product of linear factors, we have that :

`g(x)=(x+1)(x^2\text{ + 6x + 6 )}`