We have a normally distributed population with a mean of 75 and a standard deviation of 125. The probability of finding a female with a pulse rate smaller than 82 is given by the area under the curve of the corresponding normal distribution from negative infinte to 82. In order to find this area first we need to pass from our normal distribution to one with a mean value of 0 and a standard deviation of 1. In order to do this we do the following calculation:
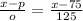
So we take x=82:
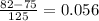
This value is known as the z value. It indicates the value of 82 in the [0,1] normal distribution. The following step is to look for this value in a z-table. Since 0.05 is the closest smaller value to 0.056 in the table we choose it:
So for a z value of 0.05 the table give us the number 0.5199. This means that the area under the curve between negative infinite and 82 beats per minute is 0.5199*total area under the curve. This means that the probability to find a female with a pulse under 82 beats is 0.5199. As a percentage it would be 51.99%.