Question

The lengths of a professor's classes has a continuous uniform distribution between 50.0 min and 52.0 min. If one such class is randomly selected, find the probability that the class length is less than 51 min. P(X < 51) = (Report answer accurate to 2 decimal places .)

Answer 1

Step-by-step explanation

If the lengths of the classes have a continuous uniform distribution between 50min and 52min then that means that the curve of its probability function is a horizontal line above the interval [50,52]. The hegiht of this line is such that the area between itself and the x-axis is equal to 1. Then the height h must meet:

`1=h\cdot(52-50)=2h\rightarrow h=(1)/(2)`

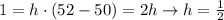
Then the graph of this distribution forms a rectangle:

The probability that the duration of a class is less than 51 minutes is equal to the probability of it having a length between 50 min and 51 min. This basically means that the probability we are looking for is equal to the area between the probability function graph (blue line) and the x-axis between 50 and 51. So basically we must find the area of this rectangle in red:

This rectangle has a base of 1 and a height of 0.5 so its area is:

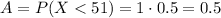
`A=P(X<51)=1\cdot0.5=0.5`Answer

Then the answer is 0.50