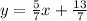The slope-intercept form of the equation of a line is:
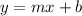
where m is the slope and b is the y-intercept.
We can find the slope m of a line passing through points (x₁,y₁) and (x₂,y₂) using the formula:
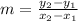
Thus, for the points (-4,-1) and (3,4), we have:
x₁ = -4
y₁ = -1
x₂ = 3
y₂ = 4
Then, we find:
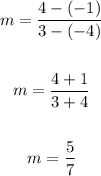
So, the equation we found so far is:
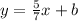
Now, we can find the value of b by replacing x and y with the coordinates of the point (3,4):
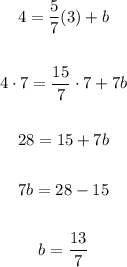
Therefore, the answer is: