Solution
Given that Plane A departs at a 41° angle from the runway while plane B departs at a 43° angle from the runway.
h stands for the height of the planes above the ground
x stands for the distance of plane A away from the airport.
y stands for the distance of plane A away from the airport.
When h = 5, we shall calculate their respective x
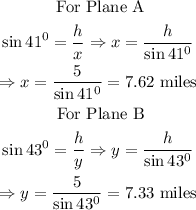
From the above calculation, we can see that Plane A what 7.62 miles away from the airport while Plane B was 7.33 miles away from the airport.
Since 7.62 > 7.33;
Therefore, Plane A was farther away from the airport when it was 5 miles from the ground.