Question

Let f(x)=-6 and g(x)=x^2. Perform the function operation and then find the domain of the result. (f-g)(x)

Answer 1

`\begin{gathered} (f-g)(x)=-6-x^2 \\ \text{Domain: all real numbers} \end{gathered}`

Step-by-step explanation

Step 1

Let

`\begin{gathered} f(x)=-6 \\ g(x)=x^2 \end{gathered}`

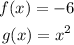
hence

`(f-g)(x)`

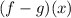
would be

`\begin{gathered} (f-g)(x)=f(x)-g(x)=-6-x^2 \\ (f-g)(x)=-6-x^2 \end{gathered}`

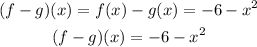
Step 2

now, let's find the domain of the function:

The domain of a function is the set of all possible inputs for the function( the x values wher the function si defined),

the solution we got is a polynomious , The domain of a polynomial is the entire set of real numbers.

so, the answer is

Domain: all real numbers

I hope this helps you