Hello!
We have the equation below:
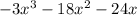
First of all, note that in all terms we have multiples of -3x. So, let's put it in evidence:
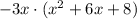
Now, let's rewrite 6x as 4x+2x:
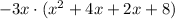
Note that we can put x in evidence because of the first and second terms, and 2 in evidence because of the third and fourth terms. Look:
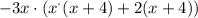
As we have (x+4) twice, let's put it in evidence too:
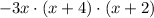
Answer:
Alternative B. -3x(x+2)(x+4)