Question

a concrete drain is 10 m long with an outside diameter of 1 m and an inside diameter of 0.8 m determine the volume of concrete required to make the drain to the nearest tenth of cubic metre

Answer 1

Let x be the volume of the cylinder with diameter 1m

Let y be the volume of the cylinder with diameter 0.8m

The volume of concrete required to make the drain is:

`V=x-y`

___________

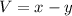
Volume of a cylinder:

`V=\pi\cdot((d)/(2))^2\cdot h`

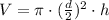
h is the height

d is the diameter

For the given drain:

`\begin{gathered} V=(\pi\cdot((d_x)/(2))^2\cdot h)-(\pi\cdot((d_y)/(2))\cdot h)_{} \\ \\ V=(((d_x)/(2))^2-((d_y)/(2))^2)\pi\cdot h \\ \\ V=(((d_x)^2)/(4)-((d_y)^2)/(4))\pi\cdot h \\ \\ V=(((d_x)^2-(d_y)^2)/(4))\pi\cdot h \\ \\ \end{gathered}`
`\begin{gathered} V=(((1m)^2-(0.8m)^2)/(4))\pi\cdot10m \\ \\ V=(1m^2-0.64m^2)/(4)\cdot\pi\cdot10m \\ \\ V=(0.36m^2)/(4)\cdot\pi\cdot10m \\ \\ V=(3.6\pi)/(4)m^3 \\ \\ V=0.9\pi m^3 \\ \\ V\approx2.8m^3 \end{gathered}`

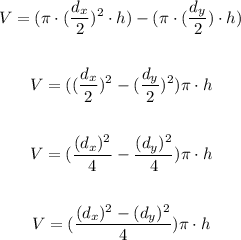
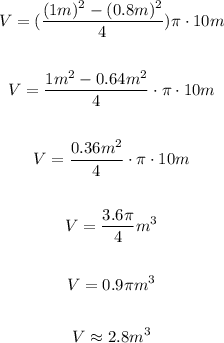
Then, the volume of concrete required is 2.8 cubic meter