This question is taken from the continuity and discontinuity in which we have to check whether a given function is continuous at the given point or not continuous, so we can write the given function below
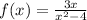
at x=4 is continuous or not.
First, we are written the given function and check whether it is continuous at a given point or not, so we have to check the left hand and right-hand limit (LHL and RHL)are equal or not, Given a function
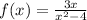
so formula we write it below at the given point
LHL=limx→−4−k(x)
RHL=limx→−4+k(x)
and applicable only limits are exist otherwise discontinuous.
RHL=LHL=k(4)
if the above formula is satisfy then the given function is continuous
now we calculate the L.H.L
LHL=limx→−4−k(x)
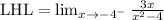
Now change the limit, x=-4-h and h=0.
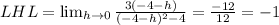
For RHL,

For x=4,
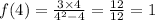
So RHL is not equal to LHL but RHL = for the function at x=4.
Then it is not satisfied the continuous property so the function is discontinuous at x=4.
So its function value is discontinuous at x= 4.