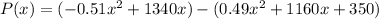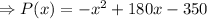We will have that:
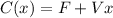
Here F is the fixed cost, V is the variable cost per unit and x the number of units; so the cost function is:
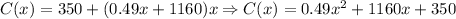
Now, we remember that the Revenue function is given by:
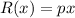
Here p is the price per item and x the number of items; so the revenue function is:
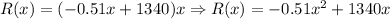
Finally, we remmeber that the profic function is given by:
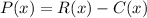
So, the profit function is given by: