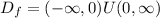Question

What is the domain of the function f(x)=4^x-3?

Answer 1

So,

We want to find the domain of the function:

`f(x)=4x^(-3)`

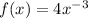
We could rewrite this function as:

`f(x)=(4)/(x^3)`

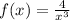
Remember that the domain of a function f(x) is defined as all the values that the variable "x" could take.

In this case, notice that if x=0, the function f is not defined. But, "x" can take any other value.

So, the domain is:

`D_f=R-\mleft\lbrace0\mright\rbrace`

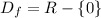
That's all the real numbers less zero.

This can be written in interval notation as:

`D_f=(-\infty,0)U(0,\infty)`