Question

Helppp. the question is in the picture. i am so stuck

Answer 1

The polynomial is given to be:

`3x^2+3x^3=6x^4`

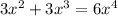
We can rewrite the polynomial to be:

`6x^4-3x^3-3x^2=0`

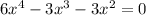
Factor the polynomial using the common factor of each term:

`\begin{gathered} Factor\Rightarrow3x^2 \\ \therefore \\ \Rightarrow3x^2(2x^2-x-1)=0 \end{gathered}`

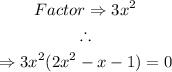
Using the Zero Factor Principle, given to be:

`\begin{gathered} If \\ ab=0 \\ \text{then} \\ a=0,b=0 \end{gathered}`

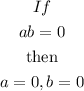
Therefore, we have:

`\begin{gathered} 3x^2=0,x^2=(0)/(3)=0,x=\pm\sqrt[]{0} \\ \therefore \\ x=0(mult.2) \end{gathered}`

or

`2x^2-x-1=0`

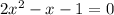
Solving using the quadratic formula given to be:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where} \\ a=2 \\ b=-1 \\ c=-1 \end{gathered}`

Therefore, we have:

`\begin{gathered} x=\frac{-(-1)\pm\sqrt[]{(-1)^2-4*2*(-1)}_{}}{2*2}=\frac{1\pm\sqrt[]{1+8}}{4}=\frac{1\pm\sqrt[]{9}}{4} \\ x=(1+3)/(4)=-(4)/(4)=1 \\ or \\ x=(1-3)/(4)=(-2)/(4)=-(1)/(2) \end{gathered}`

Therefore, the solution to the equation is:

`x=0(mult.2),1,-(1)/(2)`

Comparing our answers with the provided options, we can check for equivalent answers. From the Third Option, we have:

`\begin{gathered} x=\frac{3\pm\sqrt[]{81}}{12}=(3\pm9)/(12) \\ \therefore \\ x=(3+9)/(12)=(12)/(12)=1 \\ or \\ x=(3-9)/(12)=-(6)/(12)=-(1)/(2) \end{gathered}`

This is equivalent to the answer we got.

Therefore, the correct option is the THIRD OPTION:

`x=0(mult.2),\frac{3\pm\sqrt[]{81}}{12}`