Question

Two objects are placed so their centers are 1.35 meters apart, and the force between them is 6.19 x 10-10 newtons. What is the mass of each object if one has twice the mass of the other? Include units in your answers. Answer must be in 3 significant digits.

Answer 1

The distance between the two masses is d = 1.35 m

The force between the masses is

`F=6.19*10^(-10)\text{ N}`

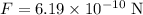
Let the mass of object 1 be m.

Let the mass of object 2 be 2m.

The formula of force can be written as

`F=(Gm*2m)/(d^2)`

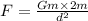
Here, the universal gravitational constant is

The mass can be calculated as

`\begin{gathered} m=(Fd^2)/(2G) \\ =(6.19*10^(-10)*(1.35)^2)/(2*6.67*10^(-11)) \\ =8.45\text{ kg} \end{gathered}`

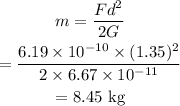
The mass of object 2 is

`2m=16.9\text{ kg}`

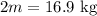
The mass of the first object is 8.45 kg.

The mass of the second object is 16.9 kg.