Question

You want to buy a $183,000 home. You plan to pay 15% as a down payment, and take out a 30 year loan for the rest. a) How much is the loan amount going to be? b) What will your monthly payments be if the interest rate is 6%? c) What will your monthly payments be if the interest rate is 7%?

Answer 1

First, let's find 15% of 183,000.

`0.15\cdot183,000=27,450`

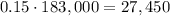
The down payment is $27,450.

(a) To find the amount of the loan, we just have to subtract.

`183,000-27,450=155,550`

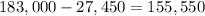
Hence, the loan amount is $155,550.

(b) The monthly payment formula is

`M=(i* P*(1+i)^n)/((1+i)^n-1)`

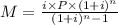
Where P = 155,550. i = 0.06/12. n = 360 (number of payments). Let's replace these values.

`\begin{gathered} M=(0.005*155,550*(1+0.005)^(360))/((1+0.005)^(360)-1) \\ M=(777.75(6.02))/(6.02-1)=(4,682.06)/(5.02)=932.68 \end{gathered}`

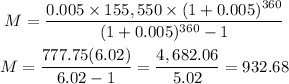
Hence, the monthly payment is $932.68.

(c) We repeat the process but instead of using 6% interest, we are going to use 7% interest.

P = 155,550.

i = 0.07/12.

n = 360.

Then, we replace the values in the formula.

`\begin{gathered} M=(0.0058*155,550*(1+0.0058)^(360))/((1+0.0058)^(360)-1) \\ M=(902.19(8.02))/(8.02-1)=(7,235.56)/(7.02)=1,030.71 \end{gathered}`

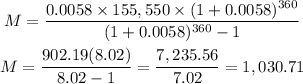
Hence, the monthly payment is $1,030.71 with 7% interest.