ANSWER:
792
Explanation:
Since there is no replacement and we assume that the order does not matter, we must use the combination formula, which is the following:
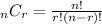
In this case n = 12 and r = 7, we substitute each value:
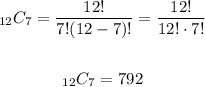
This means that there are a total of 792 different ways to choose 7 letters from 12 distinct letters.