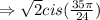Question

I need help with this practice problem solving Enter your answer by filling in the four boxes

Answer 1

The complex number to find the 4th root is given to be:

`2√(3)-2i`

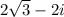
Step 1: Transform the complex number in the r.cisθ form

`\begin{gathered} r=\sqrt{(2√(3))^2+(-2)^2}=√(12+4)=√(16) \\ r=4 \\ and \\ \theta=\arctan((-2)/(2√(3)))=-(\pi)/(6) \end{gathered}`

Therefore, the polar form is:

`\Rightarrow4cis(-(\pi)/(6))`

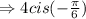
Step 2: According to the De Moivre's Formula, all n-th roots of a complex number

`\begin{gathered} rcis\theta \\ \Rightarrow r^{(1)/(n)}cis((\theta+2\pi k)/(n)) \\ for \\ k=0...n-1 \end{gathered}`

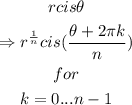
Therefore, the roots are as follows.

`n=4`

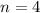
k = 0

`\begin{gathered} \Rightarrow4^{(1)/(4)}cis((-(\pi)/(6)+2\pi(0))/(4)) \\ \Rightarrow√(2)cis(-(\pi)/(24)) \end{gathered}`

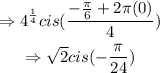
k = 1

`\begin{gathered} \Rightarrow√(2)cis((-(\pi)/(6)+2\pi)/(4)) \\ \Rightarrow√(2)cis((11\pi)/(24)) \end{gathered}`

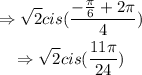
k = 2

`\Rightarrow√(2)cis((23\pi)/(24))`

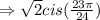
k = 3

`\Rightarrow√(2)cis((35\pi)/(24))`