Question

Please! Due soon

The table shows the test scores and the sleep averages of several students.

Test Score (%) 88 75 76 92 96 94 83 90 99 65 77 88 82 83 94 97
Average Sleep (h) 7 6.5 6 7.5 8 7 6.5 8 8.5 5 7 9 8 8.5 8.5 9

(a) Write the least squares regression equation that models the data.
Let x = the test score and y = average sleep.
(b) Use the equation to determine the approximate test score of a student who sleeps an average of 8 hours a night.
Show your work.

Answer 1

`\begin{gathered} a)\text{ }\hat{y}=-1.3385+0.104x \\ b)\text{ 89.79} \end{gathered}`

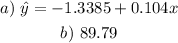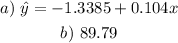
1) Let's start by making a table for that:

So now let' calculate the mean X bar , and Y bar:

`\begin{gathered} x=(88+75+76+92+96+94+83+90+99+65+77+88+82+83+94+97)/(16) \\ \bar{x}=86.1875 \end{gathered}`

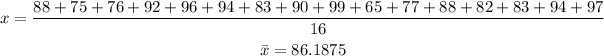
Similarly for the average of y:

`\bar{y}=7.625`

And now let's calculate the Standard Deviation for that sample Sx, and Sy:

`\begin{gathered} S_x=\sqrt[]{\frac{\sum^{}_{}(x_i-\bar{x})^2}{n-1}}=9.502411975 \\ S_y=\sqrt[]{\frac{\sum^{}_{}(y_i-\bar{y})^2}{n-1}}=1.190238071 \end{gathered}`

And finally, let's calculate the correlation coefficient: One over n-1 times the Summation of the Standard deviations of the sample:

`\begin{gathered} r=(1)/(n-1)\cdot\sum ^{}_{}(\frac{x_i-\bar{x}}{S_x})(\frac{y-\bar{y}}{S_y}) \\ r=0.8318499656 \end{gathered}`

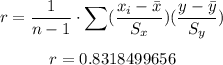
a) We can now start to write out the Least Squares Regression equation is as it follows calculating the slope

`b_1=r\cdot(S_y)/(S_x)\Rightarrow b_1=0.8318499656\cdot(1.190238071)/(9.502411975)=0.104`

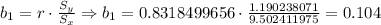
And the linear coefficient (y-intercept)

`\begin{gathered} b_0=\bar{y}-b_1\bar{x} \\ b_0=7.625-0.104\cdot86.1875 \\ b_0=-1.3385 \\ \hat{y}=-1.3385+0.104x \end{gathered}`

b) Since the number of hours of sleeping on average is given we can plug into y the number of hours to get x the score, Just like that:

`\begin{gathered} \hat{y}=b_0+b_1x \\ \hat{y}=-1.3385+0.104x \\ 8=-1.3385+0.104x \\ 8+1.3385=0.104x \\ (9.3385)/(0.104)=(0.104x)/(0.104) \\ x\approx89.79 \end{gathered}`

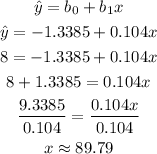
3) Hence the answer is

`\begin{gathered} a)\text{ }\hat{y}=-1.3385+0.104x \\ b)\text{ 89.79} \end{gathered}`