Answer:
To find whether the given triangles are similar, if it is similar, then to define the rule used.
Step-by-step explanation:
From the two given triangles, two corresponding angles are equal.
That is,
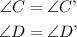
Since two corresponding angles the equal, the other angle of the triangles must be equal to each other.

we have that,
The AA criterion for triangle similarity states that if the three angles of one triangle are respectively equal to the three angles of the other, then the two triangles will be similar.
By AA rule, we conclude that the triangles are similar.
Answer is: Yes, by the AA rule.