We need to find the angle between the vectors:
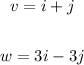
If those vectors form the sides of a triangle, then the third side is formed by the vector:

Thus, using the Law of cosines, those vectors' magnitudes are related to the angle between w and v by the formula:
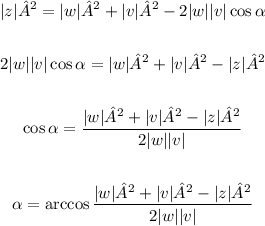
We have:

Therefore:
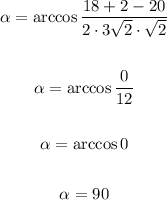
Answer: 90º