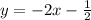Let's find the y-intercept of the line with equation
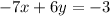
To get the y-intercept, we plug in "0" into "x". So,
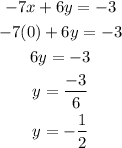
So, the coordinate point is
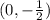
We need to find the equation of the line that is perpendicular to the line with equation -2x + 4y = 2 and passes through the point (0, -1/2).
First, let's re-arrange -2x + 4y = 2 into the form y = mx + b, where m is the slope and b is the y-intercept.

We know the line perpendicular will have a slope that is negative reciprocal.
So, the perpendicular line will have a slope of
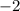
So, the line will take the form:
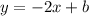
Since it goes through the point (0, -1/2), we can solve for "b":

Thus, the equation of the linne is,