Question

Please help me with this problem so that my son can understand better. Let f(x)=−0.5(x−8)^2−2.What is the average rate of change for the quadratic function from x=−4 to x = 8? Enter your answer in the box.

Answer 1

The function is given to be:

`f(x)=-0.5(x-8)^2-2`

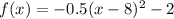
To calculate the average rate of change between two points, we can use the formula:

`\Rightarrow(f(a)-f(b))/(a-b)`

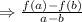
where a and b are the points.

For the function provided, we are to find the rate of change between -4 and 8. Hence, our formula will be:

`(f(-4)-f(8))/(-4-8)=(f(-4)-f(8))/(-12)`

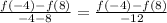
We can evaluate f(-4) and f(8) to be:

`\begin{gathered} f(-4)=-0.5(-4-8)^2-2=-0.5(-12)^2-2=-0.5(144)-2=-72-2=-74 \\ f(8)=-0.5(8-8)^2-2=-2 \end{gathered}`

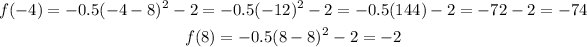
Therefore, the average rate of change is calculated to be:

`\Rightarrow(-74-(-2))/(-12)=(-74+2)/(-12)=(-72)/(-12)=6`

The average rate of change is 6.