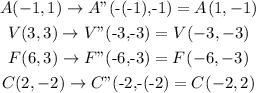Answer:
A'' = (1, -1)
V'' = (-3, -3)
F'' = (-6, -3)
C'' = (-2, 2)
Explanations:
Given the coordinate of the quadrilateral AVFC as shown:
A = (-1, 1)
V = (3, 3)
F = (6, 3)
C =(2, -2)
The rule for the 180° clockwise rotation about the origin is given as;
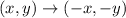
This shows that the coordinates were negated but their original position must be retained.
For the coordinate points of the quadrilateral AVFC, the 180° clockwise rotation about the origin will be given as;