Question

Carlos is a boat dealer who bought a sailboat for $13,600 and then sold it for $15,200 what percent was his markup on the boat?

Answer 1

Markup refers to the difference between the selling price of a good or service and its cost. It is expressed as a percentage above the cost.

Given:

`\begin{gathered} \text{Cost price (C.P)=\$13,600} \\ \text{Selling price (S.P)=\$15,200} \end{gathered}`

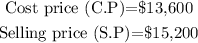
Mark up is given by;

`\begin{gathered} \text{Mark up}=S\mathrm{}P-C\mathrm{}P \\ \text{Mark up=15200-13600} \\ \text{Mark up =\$1600} \end{gathered}`

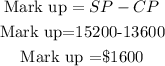
Mark up percent is;

`\begin{gathered} \text{Mark up \%=}\frac{\text{Mark up}}{C\mathrm{}P}*100\text{ \%} \\ =(1600)/(13600)*100 \\ =(1600)/(136) \\ \text{Mark up \% =11.76\%} \end{gathered}`

Therefore, the percentage mark up on the boat is 11.76%