Answer:
Explanation:
The match of the terms and definitions is given in the image below:
(1)Factorial
The factorial of a number is defined as follows:
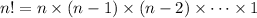
(2)Combination
When the order of arrangement does not matter, the problem is a combination problem.
(3)Sample Space
The sample space of an event is the set of all the possible outcomes in that event.
(4)Independent Events
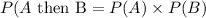
If two events, A and B are independent, then:
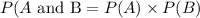
What this means is that the probability of one event does not affect the other event, so, you simply multiply the individual probabilities.
(5)Outcome
When a coin is flipped, the possible events (Heads or Tails) are referred to as the outcome of the event.
(6)Counting Principle
The number of possible ways/outcomes of an event is determined by using the counting principle.
(7)Permutation
When the order of arrangement matters, the problem is a permutation problem.
(8)Dependent Events
For any two dependent events, A and B, the conditional probability of B given A is determined using the formula::
![\begin{gathered} P(B|A)=(P(B\cap A))/(P(A)) \\ \implies P(B\text{ after A\rparen=}\frac{P(A,then\text{ }B\rparen}{P(A)} \\ \text{ Cross multiply} \\ P(A,\text{ then B}\operatorname{\rparen}=P(A)P(B\text{ after A}\operatorname{\rparen} \end{gathered}]()
(9)If Renee rolls a six-sided cube, if A is the event of rolling an even number, the sample space for A is:
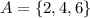
Therefore, the complement of A is:
