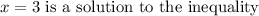Answer
x = 3
Step-by-step explanation
Given inequality:
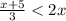
Multiply both sides of the inequality by 3 in order to clear fraction:
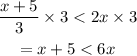
Combine the like terms
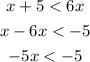
Divide both sides by -5. Note the < will change to >
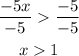
This implies the values of x must be greater than 1, i.e. in terms of whole number, x = 2, x = 3, x = 4, ......... could be any of the solutions.
Hence,