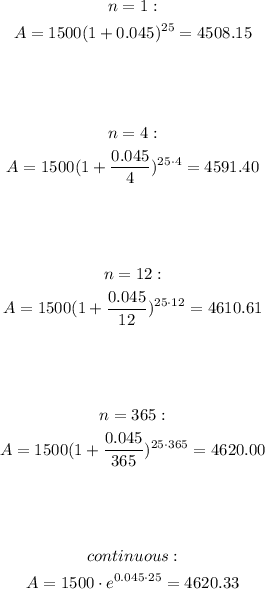Question

Complete the table to determine the balance A for P dollars invested at rate r for t years, compounded n times per year.

Answer 1

In order to calculate the balance in compound interest, we can use the formula below:

`A=P(1+(r)/(n))^(nt)`

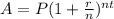
Where A is the balance after t years, P is the principal (initial amount), r is the interest rate and n is how many times the interest is compounded in a year.

For continuous compounding, we use this formula instead:

`A=P\cdot e^(rt)`

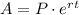
So we have:

`\begin{gathered} n=1: \\ A=1500(1+0.045)^(25)=4508.15\\ \\ \\ \\ n=4: \\ A=1500(1+(0.045)/(4))^(25\cdot4)=4591.40\\ \\ \\ \\ n=12: \\ A=1500(1+(0.045)/(12))^(25\cdot12)=4610.61\\ \\ \\ \\ n=365: \\ A=1500(1+(0.045)/(365))^(25\cdot365)=4620.00\\ \\ \\ \\ continuous: \\ A=1500\cdot e^(0.045\cdot25)=4620.33 \end{gathered}`