
53 due west
Step-by-step explanation
4.
Step 1
draw
Displacement is the change in position of an object,it is the absolute value of the displacement, because displacement is a vector and cannot have a negative value of magnitude
so
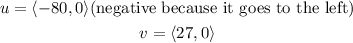
now, add the vectos to find the total displacement (D)
![\begin{gathered} D=u+v \\ D=\langle-80,0\rangle+\langle27,0\rangle=\langle-53,0\rangle \\ D=\langle-53,0\rangle \\ \text{therefore, the total displacement is}(\text{magnitude)} \\ \lvert D\rvert=\sqrt[]{(x-component)^2+(y-componte)^2} \\ \text{replace} \\ \lvert D\rvert=\sqrt[]{(-53)^2+(0)^2} \\ \lvert D\rvert=\sqrt[]{2809} \\ \lvert D\rvert=53 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/p1to6wwdpm9kwjsmcpql1rw844wl7ew5h3.png)
so, the magnitude is 53,
direction
![undefined]()
53 due west
I hope this helps you