Given:-
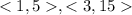
To find:-
The given vectors are parallel, orthogonal or neither.
So now we check, the given vectors is orthogonal or not.
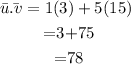
The given vectors are not orthogonal because if the vectors are orthogonal the dot product should be zero.
So now we check, the given vectors is parallel or not,
![\begin{gathered} \lvert u\rvert=\sqrt[]{1^2+5^2} \\ \text{ =}\sqrt[]{1+25} \\ \text{ =}\sqrt[]{26} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qz4x4l58vre87avkqc9sgrge1pz2d5q50m.png)
Also,
![\begin{gathered} \lvert v\rvert=\sqrt[]{3^2+15^2} \\ \text{ =}\sqrt[]{9+225} \\ \text{ =}\sqrt[]{234} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zez3y0svtgaefcwii6w2wrddowwrprb8at.png)
So now,
![\begin{gathered} \theta=\cos ^(-1)((u.v)/(\lvert u\rvert\lvert v\rvert)) \\ \theta=\cos ^(-1)(\frac{78}{\sqrt[]{26}\sqrt[]{234}}) \\ \theta=\cos ^(-1)((78)/(5.099*15.29)) \\ \theta=\cos ^(-1)(1) \\ \theta=90 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5dsibje4qej4wtjcyherce31f0c4muaylt.png)
So we get the value of theta as 90 degree. So the given vectors are Parallel.