Question

I need help with pre calculus.

Answer 1

Question 1

Answer: Choice A) -7

-----------------

Step-by-step explanation:

To compute f(g(2)), we'll first need to find g(2).

Locate 2 in the x row. Then read straight down until you get to the g(x) row. You should find that g(2) = 4

This means f(g(2)) becomes f(4). We then repeat the same process as before. Locate 4 in the x row, read straight down til you get to the f(x) row to find that f(4) = -9

Overall, we can say f(g(2)) = -9

We do the same set of steps to compute g(f(-1)). You should find that f(-1) = -1 and g(f(-1)) = g(-1) = -2

Lastly, we subtract the results we got:

f(g(2)) - g(f(-1)) = -9 - (-2) = -9+2 = -7

==============================================

Question 2

Answer: Choice B) 0

-----------------

Step-by-step explanation:

If you were to graph each equation, you should get what you see below.

The red and blue curves do not intersect in any way. We need an intersection point to have a solution. Because there are no intersections, we don't have any solutions. The system is considered inconsistent.

==============================================

Question 3

Answer: Choice B

`-2x^2+250x-2000`

-----------------

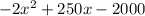
Step-by-step explanation:

x = number of scooters made and sold

Each scooter costs $150 to make. If you made x of them, then it costs 150x dollars. Then tack on the fixed cost of $2000 to get the expression
`150x+2000`

The cost function is
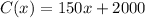`C(x) = 150x+2000`. We'll subtract this from the revenue function R(x) to get the profit P(x)

`\text{Profit} = \text{Revenue} - \text{Cost}\\\\P(x) = R(x) - C(x)\\\\P(x) = (400x-2x^2) - (150x+2000)\\\\P(x) = 400x-2x^2-150x-2000\\\\P(x) = -2x^2+250x-2000\\\\`

==============================================

Question 4

Answer: Choice B

`\left\{x\in \mathbb{R} \big| \ x \\e -2, x \\e 1\right\}`

-----------------

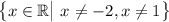
Step-by-step explanation:

`g(x) = (1)/(x+1)\\\\g(f(x)) = (1)/(f(x)+1)\\\\g(f(x)) = (1)/(x^2+x-3+1)\\\\g(f(x)) = (1)/(x^2+x-2)\\\\g(f(x)) = (1)/((x+2)(x-1))\\\\(g\circ f)(x) = (1)/((x+2)(x-1))\\\\`

I started with the outer function g(x) and replaced each x with f(x) in the second step. Then I plugged in f(x) = x^2+x-3 and simplified. Factoring the denominator is helpful to determine where the denominator becomes zero. Specifically, it happens when x = -2 and x = 1. These x values must be kicked out of the domain to avoid a division by zero error.

So we start off with the real number line, and poke holes at x = -2 and x = 1.

The notation
`x \in \mathbb{R}` means x is a real number. Then we tack on
`x \\e -2, x \\e 1`

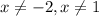
Overall, the domain is
`\left\{x\in \mathbb{R} \big| \ x \\e -2, x \\e 1\right\}`

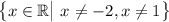
Let's see what happens if we tried plugging x = -1 into this composite function:

`(g \circ f)(x) = (1)/((x+2)(x-1))\\\\(g \circ f)(-1) = (1)/((-1+2)(-1-1))\\\\(g \circ f)(-1) = (1)/((1)(-2))\\\\(g \circ f)(-1) = (1)/(-2)\\\\(g \circ f)(-1) = -0.5\\\\`

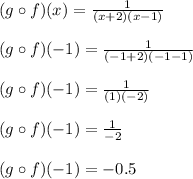
We don't get a division by zero error, so x = -1 is allowed. The same can be said about any other x value as long as it's not -2 and not 1 either.