Question

A building is 1 ft from an 8-ft fence thatsurrounds the property. A worker wantsto wash a window in the building 11 ftfrom the ground. He plans to place aladder over the fence so it rests againstthe building. (See the figure.) Hedecides he should place the ladder 7 ftfrom the fence for stability. To thenearest tenth of a foot, how long aladder will he need?

Answer 1

- In order to visualize how to solve the question, we can redraw the diagram given as follows:

- From the above, we can see that the diagram is a right-angled triangle with Opposite of 11 ft, Adjacent of 8 ft and the Hypotenuse is x (which represents the length of the ladder)

- Thus, to find the length of the ladder, x, we apply the Pythagoras theorem.

- The Pythagoras theorem is given below as follows:

`\text{Hyptoenuse}^2=\text{Opposite}^2+\text{ Adjacent}^2`

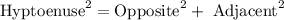
- Thus, with the above formula, we can proceed to solve the question.

- This is done below:

`\begin{gathered} x^2=8^2+11^2 \\ x^2=64+121 \\ x^2=185 \\ \text{Take the square root of both sides} \\ \\ \therefore x=\sqrt[]{185} \\ \\ x=13.60147\ldots\approx14ft\text{ (To the nearest foot)} \end{gathered}`

Final Answer

The length of the ladder to the nearest foot is 14 ft