Question

Does the quadratic function have a minimum or maximum value? What is the value, and where does it occur?

Answer 1

Given that,

The function is,

`f(x)=-x^2+2x-4`

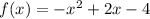
To find the minimum or maximum value.

As a 1st step, we need to find the derivative of a function f(x).

Derivative of a function f'(x) is,

`f^(\prime)(x)=-2x+2`

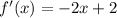
Then, consider f'(x)=0.

we get,

`-2x+2=0`
`-2x=-2`
`x=1`

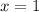
x=1 is the extremum point.

To find whether the value x=1 is minimum or maximum.

we have that, To find x=a is minimum or maximum value,

we use, if x=a-c, where f'(a-c) is positive (left point), and x=a+c, where f'(a+c) is negative (right point), then the value x=a is maximum value.

if x=a-c, where f'(a-c) is negative, and x=a+c, where f'(a+c) is positive, then the value x=a is minimum value.

where c is any positive small integer.

we consider,

x=0 (left point), Substitute in f'(x), we get

`f^(\prime)(x)=-2(0)+2`
`f^(\prime)(x)=2`
`f^(\prime)(x)=2\text{ \lparen positive\rparen}`

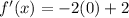
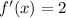
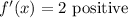
Consider x=2 (right point), Substitute in f'(x), we get

`f^(\prime)(x)=-2(2)+2`
`f^(\prime)(x)=-4+2`
`f^(\prime)(x)=-2\text{ \lparen negative\rparen}`

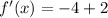
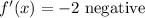
Hence x=1 is the maximum value.

The function has a maximum value.

we get that, when x=1, f(x) is,

`f(1)=-1^2+2(1)-4`
`f(1)=-5+2`
`f(1)=-3`

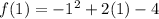
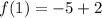
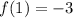
The function's maximum value is -3.

The maximum value occurs at x=1.

Answer is:

1) The function has a maximum value.

2) The function's maximum value is -3.

3) The maximum value occurs at x=1.