The first piece passes through the points (-6,-9) and (-1,-4) so the equaton of first piece is:
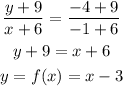
The second piece passes through the points (2,-5) and (3,-6) so it follows:
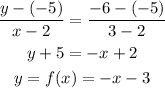
Hence the piecewise function is given by:
[tex]f(x)=\begin{cases}x-3,-6\leq x<1 \\ -x-3,1
The above function is the required piecewise function.