Question

Here are the scores of 15 students on a history test.60, 62, 65, 70, 71, 73, 74, 74, 82, 84, 88, 89, 90, 91, 93.Notice that the scores are ordered from least to greatest.Make a box-and-whisker plot for the data.

Answer 1

Given:

The data of scores of 15 students: 60, 62, 65, 70, 71, 73, 74, 74, 82, 84, 88, 89, 90, 91, 93.

To find:

The box and whisker plot for the data.

Solution:

The box and whisker plot contains the minimum value, the first quartile, the median, the third quartile, the maximum value from the data.

Here, the minimum value of the data is 60.

Here, the data is odd. So, the median of the data is:

`\begin{gathered} Median=(n+1)/(2)th\text{ term} \\ =(15+1)/(2)th\text{ term} \\ =(16)/(2)th\text{ term} \\ =8th\text{ term} \\ =74 \end{gathered}`

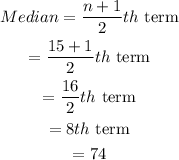
Now, the first quartile is the median of the first half. Here, the first half contains 7 elements. So, the first quartile is:

`\begin{gathered} Q1=(7+1)/(2)th\text{ term} \\ =(8)/(2)th\text{ term} \\ =4th\text{ term} \\ =70 \end{gathered}`

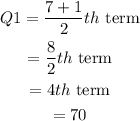
Now, the third quartile is the median of the second half. Here, the second half contains 7 elements. So, the third quartile is:

`\begin{gathered} Q2=(7+1)/(2)\text{th term} \\ =(8)/(2)th\text{ term} \\ =4th\text{ term} \\ =89 \end{gathered}`

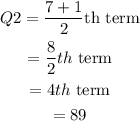
The maximum value of the data is 93.

So, the box and whisker plot for the data is given below: