Proportions
Two variables are proportional if their quotient is always a constant number. Say S and W are proportional, then:
S/W = k
where k is a constant value
From the above relation, we have:
S = k*W
In our question, S is the amount saved after W weeks of work and we know both quantities are proportional
We need to find the value of k, the proportionality constant. We do that by using the values:
S = $135 when W = 3 weeks. This means that:

Solving for k:
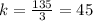
This means Jeremiah saves $45 per week. The equation now becomes:
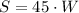
LEt's calculate the amount saved S after W=8 weeks of work:
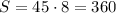
Answer: Jeremiah would save $360 in 8 weeks