Question

a point -2, 6 is rotated clockwise about the origin by 90 degrees and this image is reflected in the x-axis if the final point is labeled as P' then which of the following would the length of PP"

Answer 1

The given point is P(-2, 6).

The rule for a 90 degrees clockwise rotation is

`(x,y)\rightarrow(y,-x)`

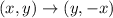
So, using the rotation rule P' is (6, 2).

The rule for a reflection across the x-axis is

`(x,y)\rightarrow(x,-y)`

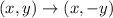
So, using this reflection rule, P'' is (6, -2).

Hence, the final point is P''(6, -2).

Then, we find the length PP''.

`\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)} \\ d=\sqrt[]{(-2-6)^2+(6-(-2))^2} \\ d=\sqrt[]{(-8)^2+(8)^2}=\sqrt[]{64+64} \\ d=\sqrt[]{128} \end{gathered}`

Hence, the answer is 2).