Question

I need help with these 2 problems, my teacher would like fractions to help explain how I got it... Example (56/100=45/64) =) Thank you in advance!!

Answer 1

We operate as follows:

**First problem:

*We divide the total number of messes by the value of the sum of the ratio.

391 / (14 + 9) = 17

After that, we multiply this value times the ration for the Gooey messes and we will obtain the number of Gooey messes present in the 391 messes:

17 * 14 = 238

So, we can expect 238 Gooey messes.

**Second problem:

*We have 174 purple yogi berries; we will have to calculate the number of berries that represent the 76% if we want to know how many are not purple. We also have the following ration 24:76 here there are 24 purple yogi berries to 76, not purple yogi berries, now we calculate:

`(24)/(76)=(174)/(NP)\Rightarrow NP=(174\cdot76)/(24)\Rightarrow NP=551`

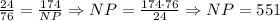
So, we would expect 551, not purple yogi berries.