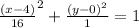Solution
Writing an equation of an ellipse given the center and endpoint of an axis
Let center C ; C(h=4; k= 0)
Let the length of its major axis AA’=2a=8 ; a=4
Let the length of its minor axix BB’=2b=?
B(4 ; 0) ; C(4 ; - 1) ; BC=b

The equation of ellipse in standard form when it is horizontal is :
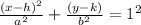
Therefore the equation of the ellipse is