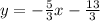Question

Please help me find the equations for the parallel line and the perpendicular line. :(

Answer 1

Given the equation of a line, you can find the equation of a line perpendicular to it, knowing the following: The product of the slopes of the lines is -1, it means that:

`m1\cdot m2=-1`

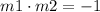
We already know the value of the first slope (which is the slope of the given line). Use this value to find the slope of the perpendicular line:

`\begin{gathered} -(5)/(3)\cdot m2=-1 \\ m2=-1\cdot-(3)/(5) \\ m2=(3)/(5) \end{gathered}`

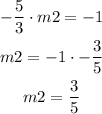
The slope of the perpendicular line is 3/5. Use this slope and the given point, to find the equation of the perpendicular line using the point slope formula, this way:

`\begin{gathered} y-y1=m(x-x1) \\ y-4=(3)/(5)(x-(-5)) \\ y-4=(3)/(5)x+3 \\ y=(3)/(5)x+7 \end{gathered}`

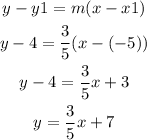
The equation of the perpendicular line is:

`y=(3)/(5)x+7`

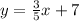
To find the equation of the line that is parallel to the given line, use the following information: parallel lines have the same slope, it means:

`m1=m2`

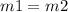
m1 has a value of -5/3, it means the parallel line also has a slope of -5/3.

Use this slope and the given point in the point slope formula, this way:

`\begin{gathered} y-4=-(5)/(3)(x-(-5)) \\ y-4=-(5)/(3)x-(25)/(3) \\ y=-(5)/(3)x-(25)/(3)+4 \\ y=-(5)/(3)x-(13)/(3) \end{gathered}`

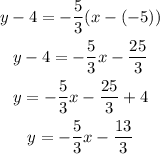
The equation of the parallel line is:

`y=-(5)/(3)x-(13)/(3)`