Question

Use the image to determine which pair of lines, if any, are parallel.

Answer 1

They give us a lot of information about the angles, first, let's suppose that a is not parallel to b, and see what happens to the angles:

Consider the same number for angles. Note that if c//d and a are not parallel to b then the angles 2 and 10 would be different, but 2 and 10 are equal. Therefore a is parallel to b. a//b

Now let's see what happens if a//b and c are not parallel to d.

In that case, the angles 1 and 16 would be different too, and as we can see they're not, then, all the lines are parallel, a is parallel with b, and c is parallel with d.

A with that we can confirm that

`\angle1\cong\angle3\cong\angle6\cong\angle8\cong\angle9\cong\angle14\angle\cong\angle11\cong\angle16\cong`

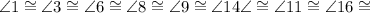
They're all the same angle

`\angle2\cong\angle4\cong\angle5\cong\angle7\cong\angle10\cong\angle12\angle\cong\angle13\cong\angle15\cong`

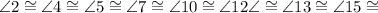
18)

Here he asks if the angle 7 is equal to the angle 12, if the lines are all parallel we have something like

We know that angle 7 is equal to angle 4 because it's opposite by a vertex. But look that we have the same pattern here

See that angle 15 is equal to angle 7, but angle 15 is also equal to angle 12. It means that angle 7 is equal to angle 12.