Question

How many moles are present in 11.0L of neon gas at STP?

Answer 1

0.49moles

Explanations:

According to the ideal gas equation

`PV=nRT`

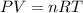
where:

• P is the ,pressure ,of the gas

,

• V is the ,volume ,of the gas

,

• n is the ,number of moles

,

• R is the ,Gas constant

,

• T is the ,temperature, (in Kelvin)

Given the following parameters at STP

`\begin{gathered} P=1atm \\ V=11.0L \\ R=0.08205Lat\text{m/molK} \\ T=273K \end{gathered}`

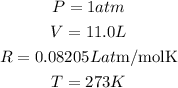
Determine the required number of moles

`\begin{gathered} n=(PV)/(RT) \\ n=(1atm*11.0L)/(0.08205*273) \\ n=(11)/(22.399) \\ n=0.49moles \end{gathered}`

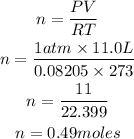
Hence the number of moles present in 11.0L of neon gas at STP at 0.49moles