The amount of money in the savings account 't' years after 2015 is given by,
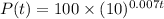
Solve for P(0) as,
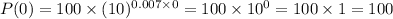
It means, at the beginning of the tenure, i. e. year 2015, the account had $100 only.
The time taken for the account to have $140 is calculated as,
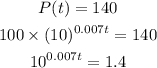
Take common logarithms on both sides,
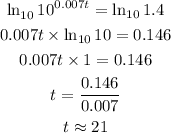
Thus, it will take arount 21 years for the account to have $140.