Question

Simplify the following expression to simplest form using only positive exponents. 1

Answer 1

For this problem, we need to simplify a certain expression using only positive exponents.

The expression is given below:

`(16x^(-32)y^(-12))^{(5)/(4)}`

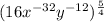
The first step is to multiply the exponent that is outside of the parenthesis with the ones inside the parenthesis.

`\begin{gathered} 16^{(5)/(4)}x^{(-32\cdot5)/(4)}y^{(-12\cdot5)/(4)}\\ \\ 16^{(5)/(4)}x^(-40)y^(-15) \end{gathered}`

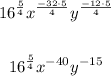
Now we need to invert the two bases, to make the exponents positive:

`\begin{gathered} \frac{16^{(5)/(4)}}{x^(40)y^(15)}\\ \\ \frac{\sqrt[4]{16^5}}{x^(40)y^(15)}\\ \\ (32)/(x^(40)y^(15)) \end{gathered}`