Given:
The measures of the sides of the rectangle are (2x+7) and (5x+9).
Aim:
We need to find the area of the given rectangle.
Step-by-step explanation:
A)
Let the length of the rectangle, l=2x+7.
Let the width of the rectangle, w =5x+9.
Consider the formula to find the area of the rectangle.
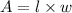
Substitute l=2x+7 and w =5x+9 in the formula.
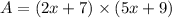
Multiply (2x+7) and (5x+9) as follows.
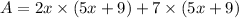
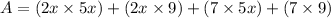

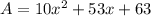
Answer:
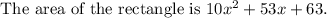
B)
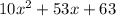
Here variable is x and the highest power of the variable x is 2.
We know that the highest power of the variable is degree.
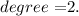
This expression contains three terms.
We know that an algebraic expression containing three terms is trinomial.
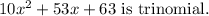
Answer:
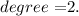
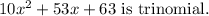
C)
Consider the polynomials (2x+7) and (5x+9).
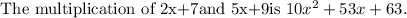
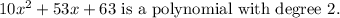
The multiplication of the polynomial is polynomial,
It gives the closure property of the polynomials by multiplication.