Given:
Diameter, D = 10.0 m
Distance, x = 7.38 x 10¹⁰ m
Wavelength, λ = 633 nm
Let's find how far apart the closest objects it could possibly resolve.
First, apply the formula for the angle for angle separation (limit of resolution):
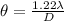
Thus, we have:
![\begin{gathered} \theta=(1.22*633*10^(-9))/(10.0) \\ \\ \theta=\frac{7.7226\operatorname{*}10^(-7)}{10.0} \\ \\ \theta=7.7226\operatorname{*}10^(-8)\text{ rad} \end{gathered}]()
Now, to find the distance of the closest objects, we have:
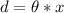
Thus, we have:
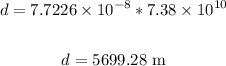
Therefore, the distance of the closest objects is 5699.28 meters.
• ANSWER:
5699.28 m