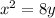Let S(h,k) be the coordinate of any point on the parabola.
It is known that the distance from any point on the parabola to its focus and to the directrix is equal.
Distance between the point and the focus is
![\sqrt[]{(h-0)^2+(k-2)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/efbeh5t0nr4col6t8g6l2akts5vxy20uh1.png)
Distance between the point and the directrix is

On equating,
![\begin{gathered} \sqrt[]{(h-0)^2+(k-2)^2}=(k+2) \\ h^2+(k-2)^2=(k+2)^2 \\ h^2=(k+2)^2-(k-2)^2 \\ h^2=8k \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wwb59611s24nsj02ok1rkbt7ov70z1gbgs.png)
So, the equation of the parabola is