Question

6x - 48 = -15y2x + 5y = 16

Answer 1

Let's begin by listing out the information given to us:

`\begin{gathered} 6x-48=-15y-----1 \\ 2x+5y=16-------2 \end{gathered}`

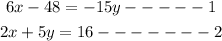
We will solve these equation simultaneously following these steps:

I. We will pick a number to multiply the equation such that the values of corresponding variables are equal

`\begin{gathered} 6x-48=-15y-----1 \\ 2x+5y=16-------2 \\ \text{Multiply equation 2 by 3, so we can eliminate the x variable} \\ 6x+15y=48------3 \\ \text{Combine equations 1 \& 3, we have:} \\ 6x-48=-15y-----1 \\ 6x+15y=48------3 \end{gathered}`

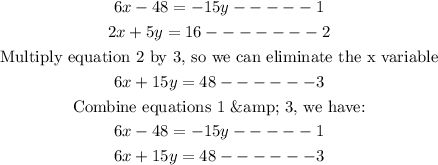
II. Subtract equation 3 from 1, we have:

The solution for these equations is non-existent