Question

Hello, I need some assistance with this homework question, please? This is for my precalculus homework. Q22

Answer 1

Step-by-step explanation

Step 1

Domain:

The domain of a function is the complete set of possible values of the independent variable,

so, we need to check the values that make the function undefined

`R\lparen x)=(x)/(x^2-100)`

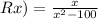
this function is undefined when the denominator equals zero, so

`\begin{gathered} x^2-100=0 \\ x^2=100 \\ x=\pm10 \end{gathered}`

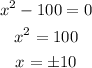
therefore, the domain is all real numbers excep 10 and -10, in set notation it is

`\begin{gathered} \lbrace x\left|x\\e10\text{ and x}\\e-10\rbrace\right? \\ \end{gathered}`

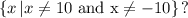
so, the answer is B

`B)\lbrace x\lvert\rvert x10\text{andx}-10\rbrace`

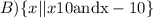
Step 2

(b) vertical asymptote

Vertical asymptotes are vertical lines which correspond to the zeroes of the denominator of a rational function.

so, the vertical asymptetes are

`\begin{gathered} x=-10 \\ x=10 \end{gathered}`

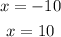
so, the answer is

`x=-10,10`

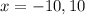
Step 3

c) horizontal asymptote

A horizontal asymptote is a y-value on a graph which a function approaches but does not actually reach.

to check the H.A.

we can use the expression

`R\left(x\right)=(p\left(x\right))/(q\left(x\right))`

`y=\frac{Leading\text{ coefficient of P\lparen x})}{Leading\text{ coefficient of Q\lparen x})}`
`\begin{gathered} if\text{ degree of P\lparen x})\text{ is}<\text{ degree of q\lparen x}) \\ the\text{ asymptote is y}=0 \end{gathered}`

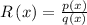
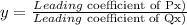
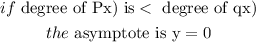
so, the horizontal asymptote is

`y=0`

Step 4

therefore, the answer is B

I hope this helps you