Question

In GHI, the measure of

Answer 1

Let's put more details in the given figure to better understand the problem:

Let's recall the Cosecant Function:

`\text{ Cosecant }\theta\text{ = }\frac{1}{\text{ Sine }\theta}\text{ = }\frac{\text{ 1}}{\text{ }\frac{\text{ Opposite Side}}{\text{ Hypotenuse}}}\text{ = 1 x }\frac{\text{ Hypotenuse}}{\text{ Opposite Side}}\text{ = }\frac{\text{ Hypotenuse}}{\text{ Opposite Side}}`

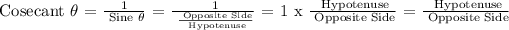
As you can see in the figure, the opposite and adjacent sides change positions from the standard one.

Because it depends on which interior angle it is being projected. Since we are projecting at ∠H, HI becomes the adjacent side and IG becomes the opposite side.

Let's now find the ratio of Cosecant ∠H.

`\text{Cosecant }\theta\text{ = }\frac{\text{ Hypotenuse}}{\text{ Opposite Side}}`
`\text{Cosecant }\angle H\text{= }\frac{\text{ GH}}{\text{ IG}}\text{ = }(65)/(56)`
`\text{Cosecant }\angle H\text{= }(65)/(56)`

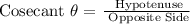
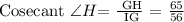
Therefore, the ratio is 65/56.