Question

I would like help solving question number two. Please be patient when answering as I will be taking notes from the answer screen. Thank you for your help.

Answer 1

STak

Hello there. To solve this question, we'll have to remember some properties about exponential growth and solving exponential equations, inequalities.

Given the colonies A and B, for which the number of bacteria are, respectivelly, modelled by the equations:

`\begin{gathered} A(t)=12e^(0.4t) \\ B(t)=24e^(kt) \end{gathered}`

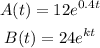
For t > 0 in hours. We have to determine:

a) The number of bacteria in colony A after 4 hours.

For this, we take t = 4 and calculate the following number:

`A(4)=12\cdot e^(0.4\cdot4)=12\cdot e^(1.6)`

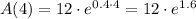
Using a calculator, we get the approximation:

`A(4)\approx59\text{ bacteria}`

b) How long does it take for the number of bacteria in colony A to reach 400?

For this, we have to determine t such that:

`A(t)=400`

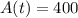
Hence plugging the exponential function, we get

`12e^(0.4t)=400`

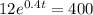
Divide both sides of the equation by a factor of 12

`e^(0.4t)=(100)/(3)`

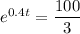
Take the natural logarithm on both sides of the equation

`\ln(e^(0.4t))=\ln\left((100)/(3)\right)`

Apply the following property:

`\log_a(a^b)=b\cdot\log_a(a)=b\cdot1=b`

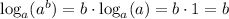
Knowing that:

`\log_e(x)=\ln(x)`

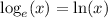
Hence we get:

`0.4t=\ln\left((100)/(3)\right)`

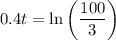
Multiply both sides of the equation by a factor of 2.5

`\begin{gathered} 2.5\cdot0.4t=2.5\cdot\ln\left((100)/(3)\right) \\ \\ t=2.5\ln\left((100)/(3)\right) \end{gathered}`

Using a calculator, we get the following approximation:

`t\approx8.76\text{ hours}`

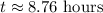
c) Find the value of k

For this, we have to use the fact that there are 60 bacteria in colony B after four hours;

Hence we get

`\begin{gathered} B(4)=60 \\ \\ 24e^(k\cdot4)=24e^(4k)=60 \end{gathered}`

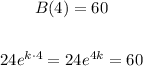
Divide both sides of the equation by a factor of 24

`e^(4k)=(5)/(2)`

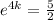
Taking the natural logarithm of both sides of the equation

`\ln(e^(4k))=\ln\left((5)/(2)\right)`

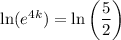
Applying the property presented before, we get

`4k=\ln\left((5)/(2)\right)`

Divide both sides by a factor of 4

`k=(1)/(4)\cdot\ln\left((5)/(2)\right)`

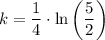
In this case it is better to keep the answer like this instead of using an approximaton.

With this, we have that B(t) will be

`B(t)=24e^{(1)/(4)\ln\left((5)/(2)\right)t}=24\cdot e^{\ln\left((5)/(2)\right)^{(t)/(4)}}=24\cdot\left((5)/(2)\right)^{(t)/(4)}`

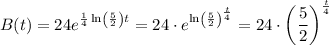
But we can keep it in the first form in order to solve part d).

d) The number of bacteria in colony A first exceeds the number of bacteria in colony B after n hours, where n is in integers. Find the value of n.

For this, we have to solve the following inequality:

`\begin{gathered} A(n)>B(n) \\ \\ 12e^(0.4n)>24e^{^{(1)/(4)\ln\left((5)/(2)\right)n}} \end{gathered}`

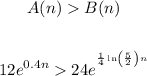
Since both exponential functions are powers of e and

`e\approx2.7182818\cdots>1`

We can solve the inequality without having to swap its order.

Divide both sides of the inequality by a factor of

`24e^(0.4n)`

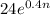
Hence we get

`e^{(1)/(4)\ln\left((5)/(2)\right)n-0.4n}<(1)/(2)`

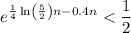
Since the logarithm is an one-to-one function, we take the natural logarithm on both sides of the inequality, preserving the order, therefore we get:

`\ln(e^{^{\left[(1)/(4)\ln\left((5)/(2)\right)-0.4\right]n}})<\ln((1)/(2))`

Applying the following property:

`\begin{gathered} \ln\left((a)/(b)\right)=\ln(a)-\ln(b),\text{ b not equal to zero;} \\ \\ \ln(1)=0 \end{gathered}`

We get that

`\ln\left((1)/(2)\right)=-\ln(2)`

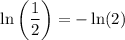
Hence we get by applying the very first property that

`\left[(1)/(4)\ln\left((5)/(2)\right)-0.4\right]n<-\ln(2)`

Divide both sides by a factor of

`(1)/(4)\ln\left((5)/(2)\right)-0.4`

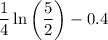
Notice it is a negative number, hence we swap the inequality sign as follows

Which evaluates to

`n>4.055`

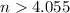
Since n is an integer, then we say

`n=5`

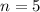
Is the first hour for which the number of bacteria on colony A exceeds the number of bacteria on colony B.