Question

A tightrope walker with a mass of 60.0 kg stands at the center of a rope which was initially strung horizontally between two poles 50.0 m apart. His weight causes the rope to sag 1.20 m. What isthe tension in the rope?

Answer 1

`T=6127.8N`

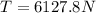
Step-by-step explanation

First, let us sketch a diagram to represent the problem:

From the diagram:

The circle represents the tightrope walker with a mass of 60kg

W represents the weight of the tightrope walker

T represents the tension on the rope

θ is the angle the sagged rope makes with the horizontal.

The vertical forces acting on the sagged rope are the tension and weight of the tightrope walker.

Notice that there are two tension forces acting on the rope, so, the vertical forces are:

`2T\sin \theta-W`

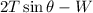
According to Newton's second law, the total vertical force must be equal to 0, so:

`2T\sin \theta-W=0`

Make T subject of formula:

`\begin{gathered} 2T\sin \theta=W \\ \Rightarrow T=(W)/(2\sin\theta)=(mg)/(2\sin \theta) \end{gathered}`

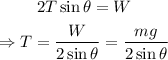
where m = mass; g = acceleration due to gravity

Applying trigonometric ratios, we have that:

`\begin{gathered} \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \\ \Rightarrow\tan \theta=(1.2)/(25)=0.048 \\ \theta=\tan ^(-1)(0.048) \\ \theta=2.75\degree \end{gathered}`

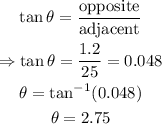
From the question:

mass, m = 60kg

This means that the tension on the rope is:

`\begin{gathered} T=(60\cdot9.8)/(2\sin (2.75)) \\ T=(588)/(0.096) \\ T=6127.8N \end{gathered}`

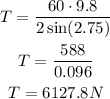
That is the answer.